Selamat datang, Pembaca Pakguru.co.id! Dalam matematika, terdapat istilah yang disebut limit, dan salah satu konsep limit yang sering dibahas adalah lim x 0 x 1. Anda mungkin pernah mendengar istilah ini, namun belum mengetahui secara detail apa itu lim x 0 x 1. Oleh karena itu, dalam artikel ini kami akan membahas tentang lim x 0 x 1 dengan rinci dan detail.
Pengenalan tentang Lim x 0 x 1
Limit adalah konsep dasar dalam kalkulus dan merupakan tema pokok yang diperkenalkan pada tahap awal perkuliahan matematika paling tinggi. Limit menyatakan nilai suatu fungsi ketika mendekati suatu titik tertentu. Lim x 0 x 1 adalah salah satu contoh limit.
Dalam matematika, nilai limit dapat diperkirakan melalui perhitungan yang cukup rumit. Namun, bila kita mencari nilai limit dengan melihat nilai fungsi tersebut saat mendekati titik asal (nol), maka kita akan mendapatkan jawaban yang mudah.
Konsep limit sangat penting dalam pengembangan dan aplikasi matematika modern. Ia digunakan dalam kegiatan sehari-hari seperti menentukan persamaan garis, menghitung turunan, dan menghitung kecepatan saat gerak.
Fungsi yang Terkait dengan Lim x 0 x 1
Dalam matematika, lim x 0 x 1 dan fungsi eksponensial berkaitan erat. Fungsi eksponensial merupakan fungsi matematika yang dinyatakan dalam bentuk f(x) = a^x, di mana a adalah bilangan positif dan bukan satu atau nol, dan x adalah bilangan real.
Saat a adalah bilangan nol, maka fungsi eksponensial akan menyamakan nilai y dengan 1. Sebaliknya, jika a adalah satu, maka fungsi eksponensial akan menyamakan nilai y dengan nilai a. Oleh karena itu, saat nilai a mendekati nol, maka nilai y akan terus mendekati nilai satu. Inilah yang memperkenalkan konsep lim x 0 x 1.
Keuntungan dari Lim x 0 x 1
Limit memungkinkan kita untuk menemukan nilai suatu fungsi ketika titik tertentu ternyata tidak dapat dicapai. Hal ini membantu kita memahami sifat fungsi tersebut saat melihat nilai fungsi pada interval yang berdekatan di sekitar titik tertentu.
Konsep limit juga membantu kita untuk memprediksi perilaku suatu sistem yang rumit tanpa melakukan perhitungan matematika yang sangat kompleks. Oleh karena itu, konsep limit sangat berguna dalam kehidupan nyata dan ilmu pengetahuan.
Kekurangan dari Lim x 0 x 1
Kekurangan dari konsep lim x 0 x 1 adalah bahwa ia mungkin membuat orang menganggap limit sebagai fungsi matematika yang diketahui nilai pastinya. Padahal limit sebenarnya menginformasikan nilai suatu fungsi saat mendekati nilai tertentu saja. Ini dapat menjadi perhatian besar pada aspek penggunaan teori limit dalam kalkulus.
Kekurangan lainnya adalah bahwa dalam beberapa situasi, “mendekati” nilai suatu fungsi dalam satu arah tertentu mungkin tidak mencerminkan perilaku fungsi saat ingin mengevaluasi fungsi di titik tersebut.
Pengetahuan Lanjutan tentang Lim x 0 x 1
Fungsi Trigonometri
Fungsi trigonometri adalah fungsi matematika yang digunakan untuk mengukur sudut. Fungsi tersebut umumnya ditulis sebagai f(x) = sin x atau f(x) = cos x, di mana x adalah sudut tertentu dalam radian.
| Sinus | Cosinus |
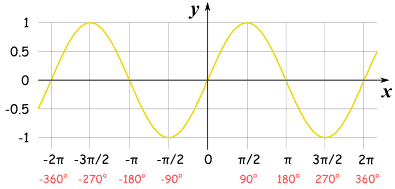 |
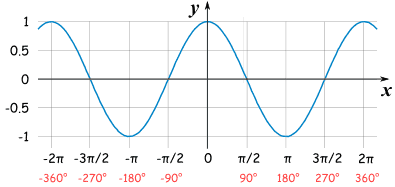 |
Nilai limit untuk fungsi trigonometrik saat menghadapi nilai seperti 0 atau pi/2 sangat mendekati nilai asimtotik daripada nilai aslinya.
Misalnya, saat memasukkan nilai pi/2 pada fungsi cosinus, maka nilai yang diperoleh adalah nol. Sementara bila kita memasukkan nilai yang sangat kecil seperti 0, maka kita akan mendapatkan nilai satu. Ini membantu kita untuk mendapatkan jawaban dari nilai fungsi trigonometrik yang benar meskipun nilai awalnya sangat kecil atau mendekati nol.
Fungsi Logaritmik
Fungsi logaritmik adalah fungsi matematika yang bertujuan untuk menghitung jumlah bilangan yang dibutuhkan untuk memperoleh hasil tertentu. Fungsi logaritmik umumnya ditulis sebagai f(x) = log a x, di mana a adalah dasar logaritma dan x adalah bilangan yang memiliki bilangan pangkat tertentu dengan dasar logaritma a.
| Logaritma Dasar 2 | Logaritma Natural |
 |
Saat x mendekati nol, log a x juga mendekati nilai negatif tak hingga. Namun, saat x mendekati tak hingga, log a x juga mendekati nilai tak hingga.
Fungsi Aljabar
Fungsi aljabar adalah fungsi matematika yang berisi suku-suku polinomial. Fungsi ini umumnya ditulis sebagai f(x) = a_n x^n + a_n-1 x^(n-1) + …+ a_1 x + a_0, di mana a_i adalah koefisien aljabar dan n adalah derajat dari polinomial.
Saat limit x mendekati nol, suku yang dominan adalah suku tertinggi. Oleh karena itu, kita dapat mencari nilai limit dengan mempercayai bahwa lim x 0 x 1 mendekati nol dengan koefisien suku yang tertinggi.
Pertanyaan Umum tentang Lim x 0 x 1
1. Apa yang dimaksud dengan limit dalam matematika?
Limit adalah nilai yang diperkirakan suatu fungsi saat mendekati suatu titik tertentu. Konsep limit digunakan dalam berbagai macam bidang matematika seperti kalkulus, geometri, dan aljabar.
2. Mengapa konsep lim x 0 x 1 penting dalam matematika?
Konsep lim x 0 x 1 memungkinkan kita untuk memahami nilai suatu fungsi saat mendekati suatu titik tertentu tanpa harus mengetahui nilai pastinya. Hal ini berguna dalam pemodelan dan perkiraan perilaku sistem matematika yang rumit.
3. Bagaimana cara mencari nilai limit suatu fungsi?
Mencari nilai limit suatu fungsi yang rumit dapat dilakukan melalui perhitungan matematika yang rumit. Namun, bila kita mencari lim x 0 x 1, maka kita dapat mencari nilai fungsi saat mendekati titik asal (nol) untuk mendapatkan jawaban yang mudah.
4. Apakah lim x 0 x 1 selalu bertambah saat suatu fungsi mendekati nol?
Tidak selalu. Nilai limit bervariasi tergantung pada sifat fungsi yang diperiksa. Ada beberapa fungsi yang nilai limitnya mendekati nol, sementara ada juga yang tidak.
5. Bagaimana lim x 0 x 1 berkaitan dengan fungsi trigonometrik?
Nilai limit untuk fungsi trigonometrik saat menghadapi nilai seperti 0 atau pi/2 sangat mendekati nilai asimtotik daripada nilai aslinya. Hal ini membantu kita untuk mendapatkan jawaban dari nilai fungsi trigonometrik yang benar meskipun nilai awalnya sangat kecil atau mendekati nol.
6. Apakah konsep limit selalu mendekati nilai pasti suatu fungsi?
Tidak selalu. Konsep limit menginformasikan nilai suatu fungsi saat mendekati nilai tertentu saja. Ini dapat menjadi perhatian besar pada aspek penggunaan teori limit dalam kalkulus.
7. Apa yang diartikan dengan limit tak hingga?
Limit tak hingga merupakan nilai yang diperkirakan suatu fungsi ketika nilainya mendekati nol atau tak hingga. Limit tak hingga dapat dibagi menjadi limit positif tak hingga dan limit negatif tak hingga.
Kesimpulan
Setelah mempelajari tentang lim x 0 x 1, kita dapat menyimpulkan bahwa konsep limit sangat penting dalam pengembangan dan aplikasi matematika modern. Dengan memahami konsep limit, kita dapat memprediksi perilaku suatu sistem yang rumit tanpa melakukan perhitungan matematika yang sangat kompleks.
Ada banyak contoh limit dalam matematika seperti lim x 0 x 1, lim x 0 cos x, dan lim x 0 ln x. Nilai limit untuk fungsi tersebut dapat dihitung melalui perhitungan matematika, namun bila kita mencari nilai limit saat mendekati titik asal (nol), maka kita akan mendapatkan jawaban yang mudah.
Jangan ragu untuk membaca artikel-artikel kami lainnya tentang matematika dan ilmu pengetahuan lainnya. Terimakasih telah membaca, Pembaca Pakguru.co.id.
Closing Words
Artikel ini dibuat semata-mata sebagai bahan pembelajaran saja. Tidak ada jaminan bahwa semua informasi dalam artikel ini adalah benar dan lengkap. Kami tidak bertanggung jawab atas kerugian atau kerusakan yang mungkin terjadi sebagai akibat dari penggunaan informasi dalam artikel ini. Harap tinggalkan komentar Anda terkait dengan artikel ini. Terima kasih telah membaca, Pembaca Pakguru.co.id.

